How 3D Game Rendering Works: Vertex Processing
In this first part of our deeper look at 3D game rendering, nosotros'll be focusing entirely on the vertex stage of the process. This means dragging out our math textbooks, brushing upward on a spot of linear algebra, matrices, and trigonometry -- oh yeah!
We'll ability through how 3D models are transformed and how light sources are accounted for. The differences between vertex and geometry shaders will be thoroughly explored, and yous'll get to see where tesselation fits in. To aid with the explanations, we'll use diagrams and lawmaking examples to demonstrate how the math and numbers are handled in a game. If you're not ready for all of this, don't worry -- you can go started with our 3D Game Rendering 101. Only once you're set, read on our for our outset closer wait at the world of 3D graphics.
Part 0: 3D Game Rendering 101
The Making of Graphics Explained
Part 1: 3D Game Rendering: Vertex Processing
A Deeper Dive Into the World of 3D Graphics
Part two: 3D Game Rendering: Rasterization and Ray Tracing
From 3D to Apartment 2D, POV and Lighting
Role 3: 3D Game Rendering: Texturing
Bilinear, Trilinear, Anisotropic Filtering, Bump Mapping, More
Part 4: 3D Game Rendering: Lighting and Shadows
The Math of Lighting, SSR, Ambience Occlusion, Shadow Mapping
Office 5: 3D Game Rendering: Anti-Aliasing
SSAA, MSAA, FXAA, TAA, and Others
What's the indicate?
In the world of math, a point is simply a location within a geometric space. There'due south zero smaller than a betoken, equally it has no size, so they can be used to conspicuously define where objects such equally lines, planes, and volumes showtime and end.
For 3D graphics, this information is crucial for setting out how everything will look considering everything displayed is a collection of lines, planes, etc. The image below is a screenshot from Bethesda'due south 2022 release Fallout 4:

It might be a bit difficult to come across how this is all just a big pile of points and lines, so we'll bear witness yous how the same scene looks in 'wireframe' mode. Set like this, the 3D rendering engine skips textures and effects done in the pixel stage, and draws naught but the colored lines connecting the points together.

Everything looks very different now, just we tin run across all of the lines that go together to brand up the various objects, environment, and background. Some are but a handful of lines, such as the rocks in the foreground, whereas others accept and so many lines that they appear solid.
Every indicate at the get-go and end of each line has been candy by doing a whole bunch of math. Some of these calculations are very quick and easy to practise; others are much harder. In that location are significant performance gains to be made by working on groups of points together, especially in the form of triangles, then let's begin a closer look with these.
So what's needed for a triangle?
The name triangle tells u.s.a. that the shape has 3 interior angles; to have this, we need 3 corners and 3 lines joining the corners together. The proper noun for a corner is a vertex (vertices beingness the plural word) and each one is described by a point. Since we're based in a 3D geometrical world, we use the Cartesian coordinate system for the points. This is ordinarily written in the grade of 3 values together, for instance (i, 8, -3), or more generally (x, y, z).

From hither, we tin add in two more vertices to become a triangle:

Note that the lines shown aren't really necessary - we can just accept the points and tell the arrangement that these three vertices make a triangle. All of the vertex information is stored in a face-to-face block of retention called a vertex buffer; the information almost the shape they volition make is either directly coded into the rendering plan or stored in another block of memory chosen an alphabetize buffer.
In the case of the former, the different shapes that can exist formed from the vertices are chosen primitives and Direct3D offers list, strips, and fans in the form of points, lines, and triangles. Used correctly, triangle strips employ vertices for more than one triangle, helping to heave performance. In the example below, we can run across that only 4 vertices are needed to make 2 triangles joined together - if they were separate, we'd need 6 vertices.

If you want to handle a larger collection of vertices, e.one thousand. an in-game NPC model, and so it's best to use something called a mesh - this is another block of retentiveness just it consists multiple buffers (vertex, index, etc) and the texture resources for the model. Microsoft provides a quick introduction to the use of this buffer in their online documents resource.
For at present, allow's concentrate on what gets washed to these vertices in a 3D game, every time a new frame is rendered (if you're not certain what that means, have a quick scan again of our rendering 101). Put simply, i or ii of things are done to them:
- Move the vertex into a new position
- Change the colour of the vertex
Set up for some math? Good! Because this is how these things get done.
Enter the vector
Imagine you accept a triangle on the screen and you push a primal to move it to the left. You'd naturally expect the (x, y, z) numbers for each vertex to change accordingly and they are; yet, how this is washed may seem a piddling unusual. Rather than but change the coordinates, the vast majority of 3D graphics rendering systems utilize a specific mathematical tool to get the job washed: we're talking about vectors.
A vector can exist thought of as an arrow that points towards a particular location in space and can be of any length required. Vertices are really described using vectors, based on the Cartesian coordinates, in this manner:

Notice how the blue arrow starts at ane location (in this case, the origin) and stretches out to the vertex. We've used what'due south chosen c olumn note to describe this vector, but row notation works just every bit well. You'll accept spotted that there is also one extra value - the 4th number is unremarkably labelled as the w-component and it is used to country whether the vector is being used to depict the location of a vertex (called a position vector) or describing a general direction (a direction vector). In the case of the latter, it would look like this:

This vector points in the same direction and has the same length as the previous position vector, so the (x, y, z) values will be the same; withal, the w-component is zip, rather than 1. The uses of direction vectors will become articulate afterward on in this article simply for at present, let's simply take stock of the fact that all of the vertices in the 3D scene will exist described this way. Why? Because in this format, information technology becomes a lot easier to start moving them about.
Math, math, and more math
Remember that we have a basic triangle and we want to move it to the left. Each vertex is described by a position vector, then the 'moving math' we need to do (known as transformations) has to piece of work on these vectors. Enter the adjacent tool: matrices (or matrix for one of them). This is an array of values written out a bit similar an Excel spreadsheet, in rows and columns.
For each type of transformation nosotros want to practise, there is an associated matrix to become with it, and it's but a case of multiplying the transformation matrix and the position vector together. We won't go through the specific details of how and why this happens, but we can run into what it looks similar.
Moving a vertex near in a 3D space is called a translation and the calculation required is this:

The x0 , etc values stand for the original coordinates of the vertex; the delta-x values represent how much the vertex needs to exist moved by. The matrix-vector calculation results in the two being simply added together (note that the w component remains untouched, so the final answer is still a position vector).
As well as moving things about, we might want to rotate the triangle or scale it bigger or smaller in size - at that place are transformations for both of these.


Nosotros tin can use the WebGL-powered graphics tool at the Real-Time Rendering website to visualize these calculations on an entire shape. Let'southward showtime with a cuboid in a default position:
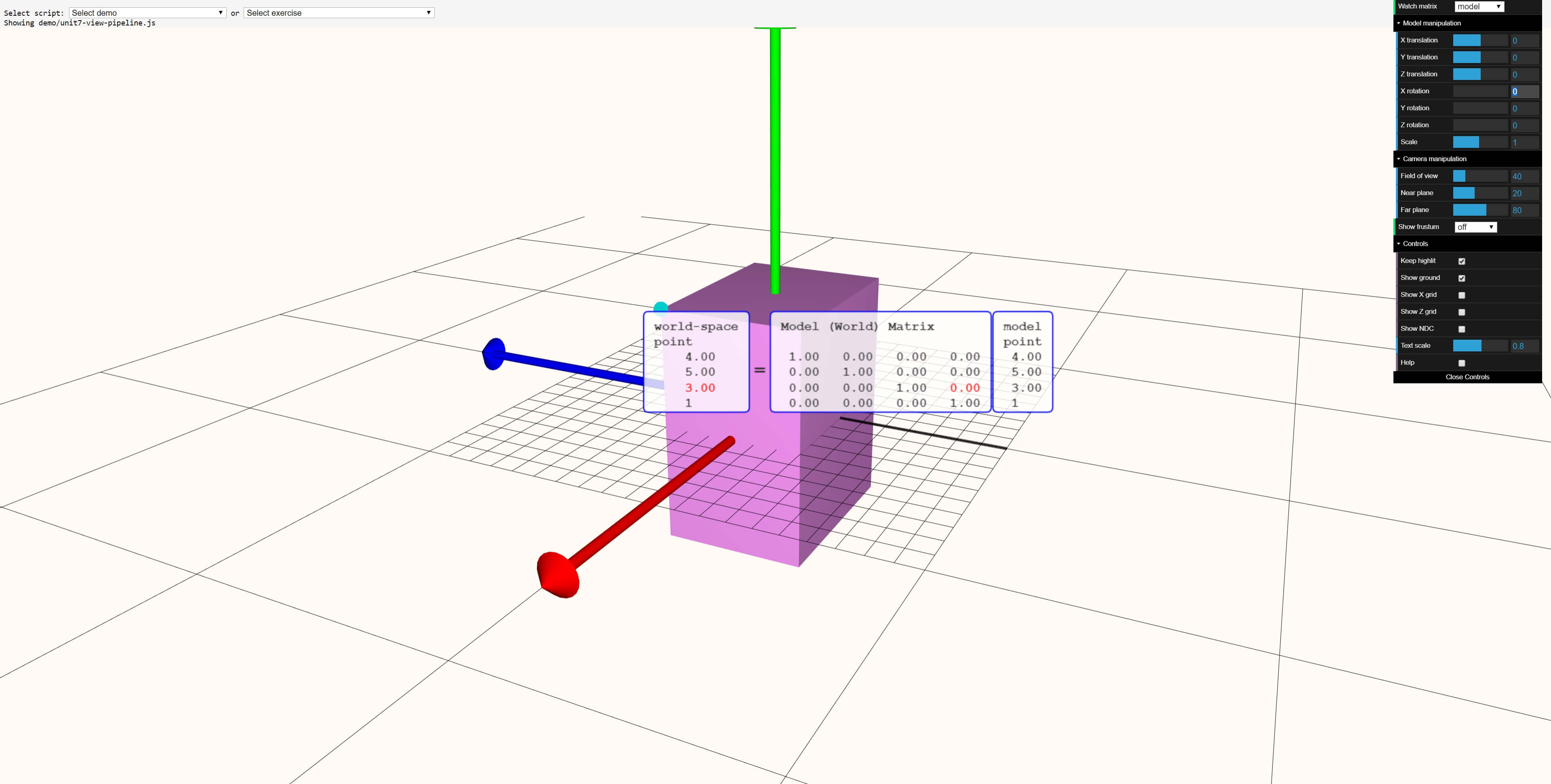
In this online tool, the model point refers to the position vector, the earth matrix is the transformation matrix, and the world-space point is the position vector for the transformed vertex.
At present let'south utilize a variety of transformations to the cuboid:
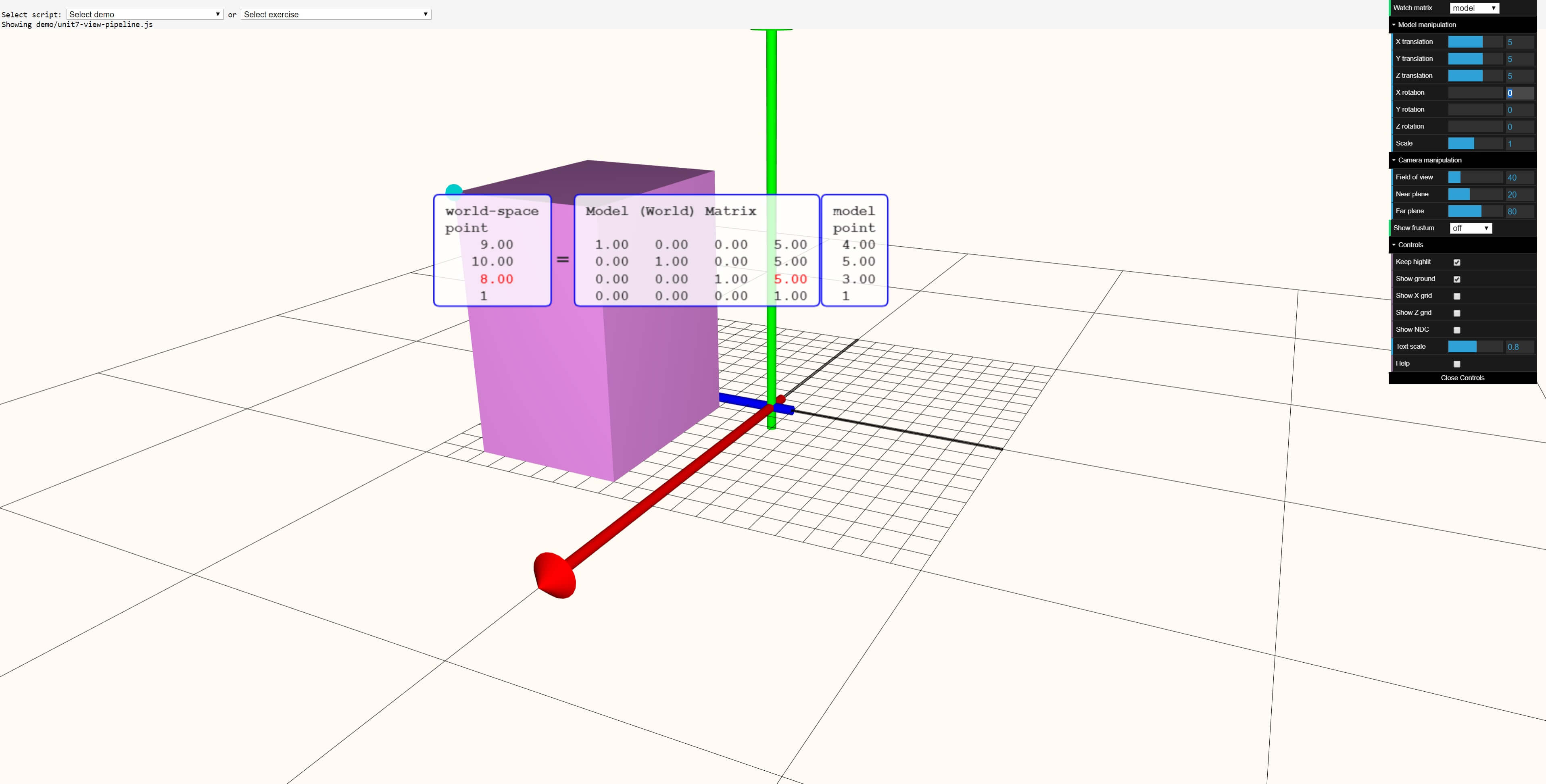
In the above image, the shape has been translated by 5 units in every direction. Nosotros can see these values in the big matrix in the heart, in the terminal column. The original position vector (4, 5, three, 1) remains the same, as information technology should, but the transformed vertex has now been translated to (9, x, eight, 1).
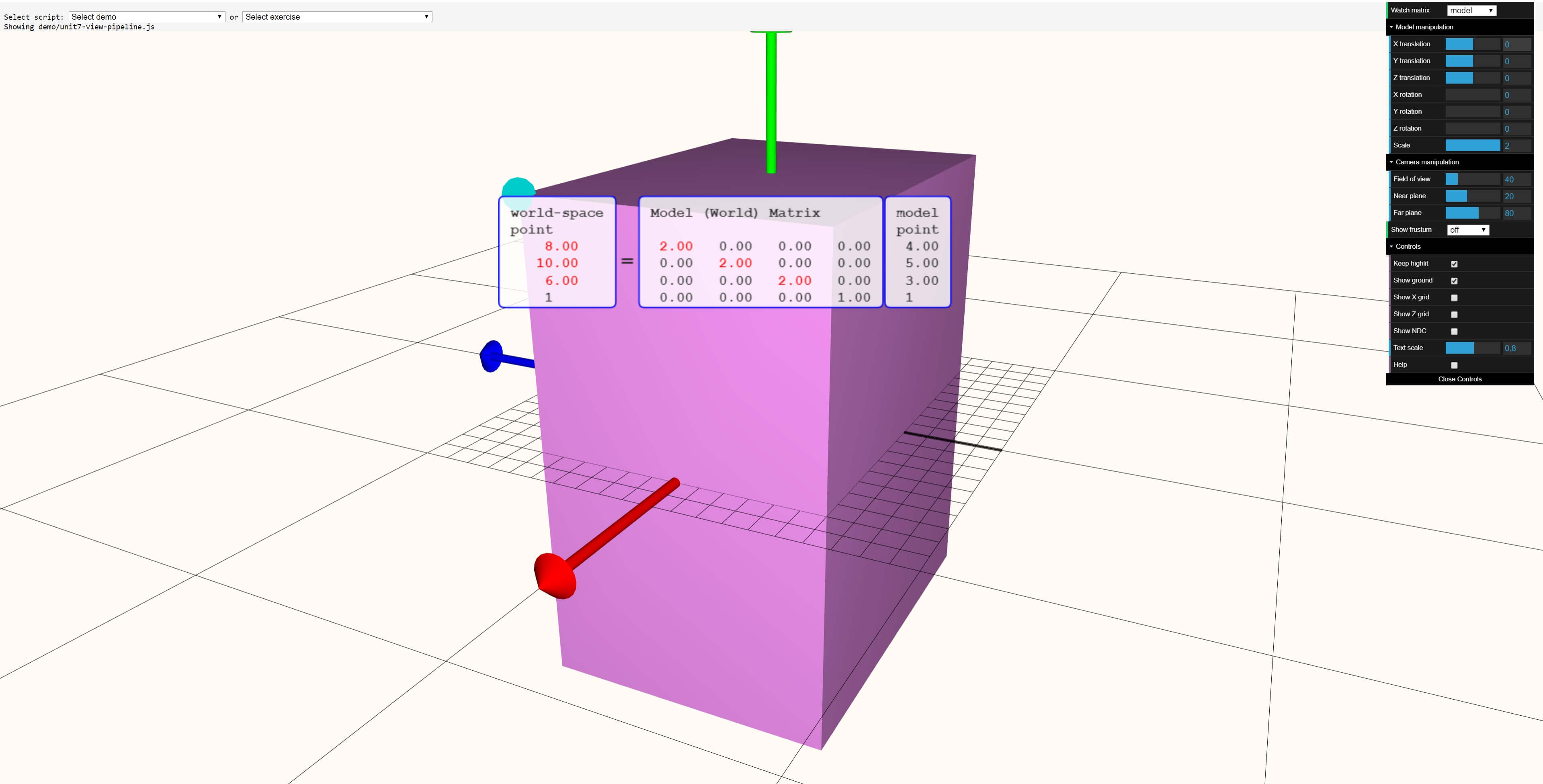
In this transformation, everything has been scaled past a factor of 2: the cuboid now has sides twice every bit long. The final instance to look at is a spot of rotation:
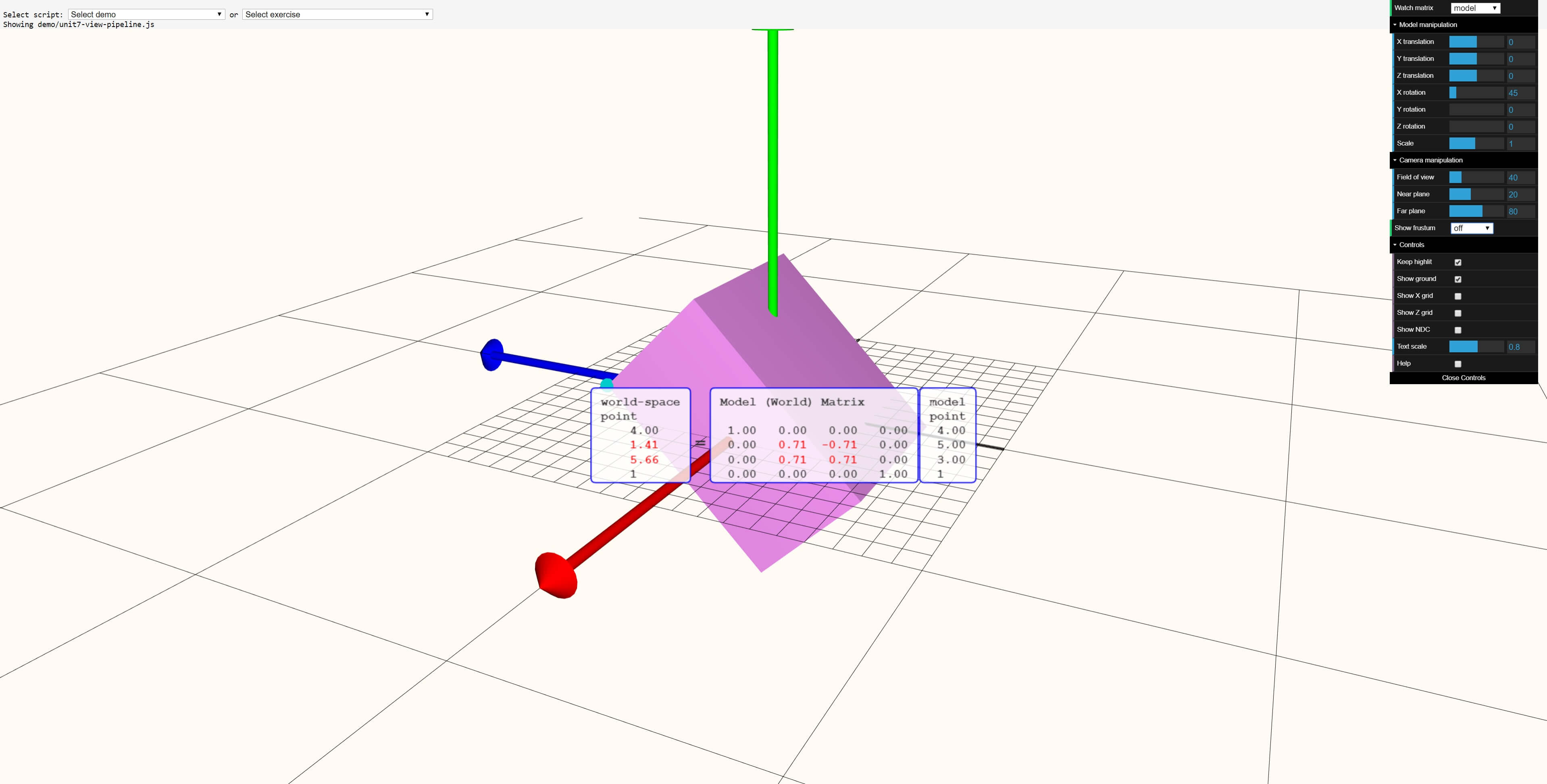
The cuboid has been rotated through an angle of 45° but the matrix is using the sine and cosine of that angle. A quick check on whatsoever scientific calculator will show u.s.a. that sin(45°) = 0.7071... which rounds to the value of 0.71 shown. We become the same answer for the cosine value.
Matrices and vectors don't have to exist used; a common culling, especially for handling complex rotations, involves the use of complex numbers and quaternions. This math is a sizeable step up from vectors, so we'll motion on from transformations.
The power of the vertex shader
At this stage we should have stock of the fact that all of this needs to be figured out by the folks programming the rendering code. If a game developer is using a tertiary-party engine (such as Unity or Unreal), then this volition have already been done for them, but anyone making their own, from scratch, will need to work out what calculations demand to be done to which vertices.
Merely what does this look like, in terms of code?
To assistance with this, we'll utilise examples from the splendid website Braynzar Soft. If yous want to get started in 3D programming yourself, it's a great identify to larn the basics, as well as some more advanced stuff...

This example is an 'all-in-one transformation'. Information technology creates the respective transformation matrices based on a keyboard input, and so applies it to the original position vector in a single operation. Note that this is e'er done in a gear up lodge (scale - rotate - translate), every bit whatsoever other manner would totally mess up the upshot.
Such blocks of lawmaking are chosen vertex shaders and they can vary enormously in terms of what they do, their size and complexity. The in a higher place example is every bit basic as they come up and arguably simply just a vertex shader, as it's non using the total programmable nature of shaders. A more complicated sequence of shaders would perchance transform it in the 3D space, work out how information technology will all appear to the scene'southward camera, and then pass that information on to the next stage in the rendering procedure. We'll look at some more than examples equally we go through the vertex processing sequence.
They tin can be used for so much more than, of course, and every time you play a game rendered in 3D but remember that all of the move yous can encounter is worked out past the graphics processor, following the instructions in vertex shaders.
This wasn't always the example, though. If we go back in time to the mid to belatedly 1990s, graphics cards of that era had no capability to process vertices and primitives themselves, this was all done entirely on the CPU.

Ane of the first processors to provide dedicated hardware acceleration for this kind of process was Nvidia'south original GeForce released in 2000 and this capability was labelled Hardware Transform and Lighting (or Hardware TnL, for short). The processes that this hardware could handle were very rigid and stock-still in terms of commands, but this quickly changed every bit newer graphics chips were released. Today, in that location is no separate hardware for vertex processing and the same units process everything: points, primitives, pixels, textures, etc.
Speaking of lighting, it's worth noting that everything we run into, of course, is because of light, so let's run into how this can be handled at the vertex stage. To exercise this, we'll utilise something that we mentioned earlier in this commodity.
Lights, camera, action!
Pic this scene: the player stands in a nighttime room, lit by a single light source off to the right. In the heart of the room, there is a behemothic, floating, chunky teapot. Okay, then we'll probably need a little help visualising this, so allow'south employ the Real-Fourth dimension Rendering website, to see something like this in action:

Now, don't forget that this object is a collection of flat triangles stitched together; this means that the plane of each triangle will be facing in a particular direction. Some are facing towards the camera, some facing the other way, and others are skewed. The calorie-free from the source will hit each airplane and bounce off at a certain angle.
Depending on where the calorie-free heads off to, the color and brightness of the plane will vary, and to ensure that the object's color looks correct, this all needs to be calculated and deemed for.
To begin with, we need to know which mode the plane is facing and for that, we need the normal vector of the plane. This is some other arrow simply dissimilar the position vector, its size doesn't matter (in fact, they are always scaled down after adding, so that they are exactly i unit in length) and it is e'er perpendicular (at a right angle) to the plane.

The normal of each triangle'south plane is calculated by working out the vector product of the two direction vectors (p and q shown in a higher place) that form the sides of the triangle. Information technology's actually amend to piece of work it out for each vertex, rather than for each individual triangle, but given that in that location will e'er be more of the onetime, compared to the latter, it's quicker just to do it for the triangles.
Once you have the normal of a surface, you can get-go to business relationship for the light source and the camera. Lights tin be of varying types in 3D rendering but for the purpose of this article, we'll only consider directional lights, e.thou. a spotlight. Like the airplane of a triangle, the spotlight and camera volition be pointing in a detail management, maybe something similar this:

The lite'southward vector and the normal vector can be used to piece of work out the angle that the light hits the surface at (using the relationship between the dot product of the vectors and the product of their sizes). The triangle's vertices volition carry additional information near their color and fabric -- in the case of the latter, information technology volition describe what happens to the calorie-free when it hits the surface.
A smooth, metallic surface will reflect most all of the incoming lite off at the same angle it came in at, and will barely change the color. By contrast, a rough, wearisome material will besprinkle the low-cal in a less predictable fashion and subtly change the color. To account for this, vertices need to have actress values:
- Original base colour
- Ambient material attribute - a value that determines how much 'background' light the vertex can absorb and reflect
- Diffuse textile attribute - another value but this fourth dimension indicating how 'rough' the vertex is, which in turns affects how much scattered light is absorbed and reflected
- Specular fabric attributes - two values giving usa a measure of how 'shiny' the vertex is
Different lighting models volition use diverse math formulae to group all of this together, and the calculation produces a vector for the outgoing light. This gets combined with the photographic camera's vector, the overall appearance of the triangle can be determined.

Nosotros've skipped through much of the finer detail here and for skilful reason: grab any textbook on 3D rendering and you'll see entire chapters dedicated to this single process. However, modern games more often than not perform the bulk of the lighting calculations and material effects in the pixel processing stage, so we'll revisit this topic in another article.

All of what we've covered so far is done using vertex shaders and it might seem that there is virtually nothing they can't do; unfortunately, in that location is. Vertex shaders tin't brand new vertices and each shader has to piece of work on every unmarried vertex. It would be handy if in that location was some style of using a fleck of lawmaking to make more triangles, in betwixt the ones nosotros've already got (to improve the visual quality) and accept a shader that works on an entire primitive (to speed things upwardly). Well, with modern graphics processors, nosotros tin can do this!
Please sir, I desire some more (triangles)
The latest graphics chips are immensely powerful, capable of performing millions of matrix-vector calculations each 2nd; they're easily capable of powering through a huge pile of vertices in no time at all. On the other hand, it's very time consuming making highly detailed models to return and if the model is going to be some distance abroad in the scene, all that actress detail will be going to waste matter.
What we demand is a style of telling the processor to break up a larger primitive, such every bit the single apartment triangle we've been looking at, into a collection of smaller triangles, all jump inside the original large one. The name for this process is tesselation and graphics chips accept been able to practice this for a good while at present; what has improved over the years is the amount of command programmers take over the functioning.
To run across this in action, we'll utilise Unigine'due south Heaven benchmark tool, as information technology allows us to apply varying amounts of tessellation to specific models used in the test.

To brainstorm with, allow'south have a location in the criterion and examine with no tessellation applied. Notice how the cobbles in the ground expect very fake - the texture used is effective but information technology just doesn't look right. Let's utilize some tessellation to the scene; the Unigine engine only applies it to sure parts only the difference is dramatic.

The ground, building edges, and doorway all now expect far more realistic. We can see how this has been achieved if we run the procedure again, only this fourth dimension with the edges of the primitives all highlighted (aka, wireframe mode):

Nosotros tin can conspicuously run into why the ground looks then odd - information technology's completely flat! The doorway is flush with the walls, too, and the edifice edges are nothing more than than elementary cuboids.
In Direct3D, primitives tin be split up into a grouping of smaller parts (a process called sub-partitioning) past running a 3-stage sequence. Offset, programmers write a hull shader -- essentially, this code creates something called a geometry patch. Think of this of beingness a map telling the processor where the new points and lines are going to appear inside the starting primitive.
Then, the tesselator unit inside graphics processor applies the patch to the primitive. Finally, a domain shader is run, which calculates the positions of all the new vertices. This data can be fed dorsum into the vertex buffer, if needed, so that the lighting calculations can be done once again, but this time with improve results.
So what does this look similar? Let's burn upward the wireframe version of the tessellated scene:

Truth exist told, we prepare the level of tessellation to a rather extreme level, to aid with the explanation of the process. Every bit good as modern graphics fries are, it's non something you'd want to practice in every game -- take the lamp post near the door, for instance.
In the not-wireframed images, you'd exist pushed to tell the difference at this altitude, and y'all can see that this level of tessellation has piled on so many extra triangles, it'due south hard to separate some of them. Used appropriately, though, and this function of vertex processing can give rise to some fantastic visual effects, especially when trying to simulate soft torso collisions.
In the non-wireframed images, you'd be pushed to tell the difference at this altitude, and you lot tin run across that this level of tessellation has piled on so many actress triangles, it'due south hard to separate some of them. Permit'southward accept a wait at how this might wait, in terms of Direct3D lawmaking; to do this, we'll use an instance from some other nifty website RasterTek.
Hither a single green triangle is tessellated into many more infant triangles...

The vertex processing is done via 3 separate shaders (encounter code example): a vertex shader to set the triangle ready for tessellating, a hull shader to generate the patch, and a domain shader to process the new vertices. The upshot of this is very straightforward only the Unigine example highlights both the potential benefits and dangers of using tessellation everywhere. Used accordingly, though, and this function of vertex processing can give ascension to some fantastic visual furnishings, particularly when trying to simulate soft torso collisions.
She can'nae handle it, Captain!
Recall the point nigh vertex shaders and that they're always run on every unmarried vertex in the scene? Information technology's not hard to see how tessellation can make this a existent trouble. And there are lots of visual effects where yous'd want to handle multiple versions of the same primitive, but without wanting to create lots of them at the showtime; hair, fur, grass, and exploding particles are all good examples of this.
Fortunately, in that location is another shader but for such things - the geometry shader. It'southward a more restrictive version of the vertex shader, but can be applied to an entire primitive, and coupled with tessellation, gives programmers greater command over large groups of vertices.

Direct3D, like all the modern graphics APIs, permits a vast array of calculations to be performed on vertices. The finalized information can either be sent onto the side by side stage in the rendering procedure (rasterization) or fed back into the memory puddle, and then that information technology tin processed again or read by CPU for other purposes. This can be done as a data stream, every bit highlighted in Microsoft's Direct3D documentation:
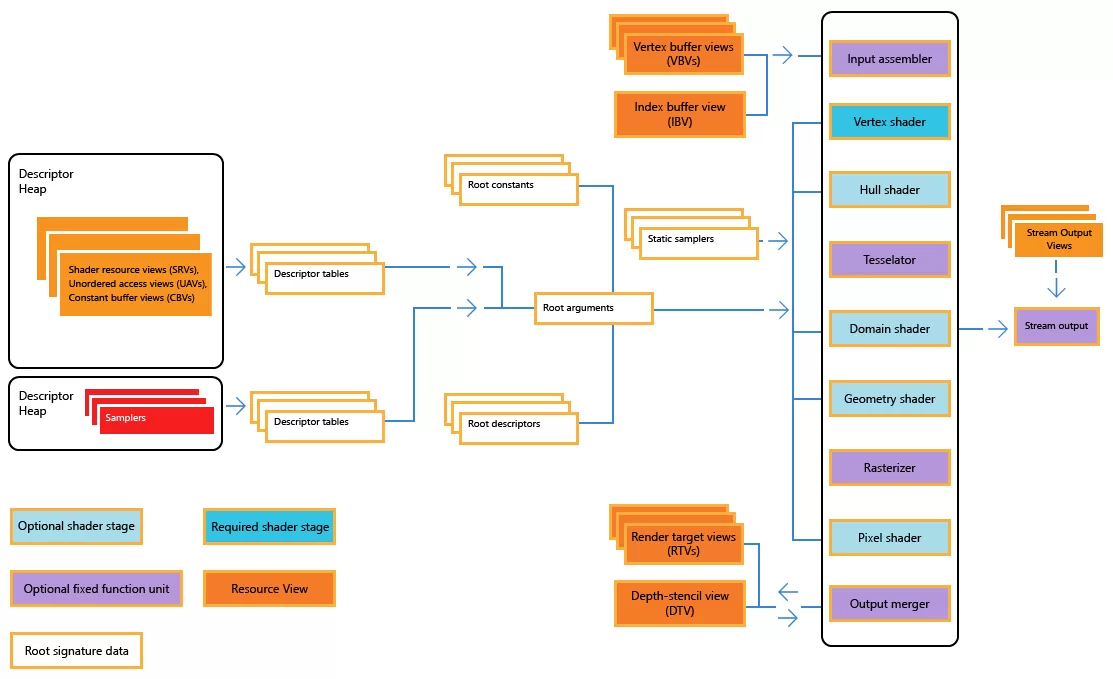
The stream output stage isn't required, specially since it can only feed entire primitives (and not individual vertices) back through the rendering loop, but information technology'southward useful for effects involving lots of particles everywhere. The same trick can exist washed using a changeable or dynamic vertex buffer, but it's improve to keep input buffers stock-still as there is performance hit if they need to be 'opened up' for changing.
Vertex processing is a critical part to rendering, as information technology sets out how the scene is arranged from the perspective of the photographic camera. Modernistic games can use millions of triangles to create their worlds, and every unmarried one of those vertices will have been transformed and lit in some way.

Handling all of this math and data might seem like a logistical nightmare, just graphics processors (GPUs) and APIs are designed with all of this in mind -- movie a smoothly running factory, firing one particular at a time through a sequence of manufacturing stages, and you lot'll have a adept sense of it.
Experienced 3D game rendering programmers accept a thorough grounding in advanced math and physics; they apply every pull a fast one on and tool in the trade to optimize the operations, squashing the vertex processing stage down into just a few milliseconds of time. And that's just the showtime of making a 3D frame -- next in that location's the rasterization phase, so the hugely complex pixel and texture processing, earlier information technology gets anywhere virtually your monitor.
Now you've reached the finish of this commodity, we hope y'all've gained a deeper insight into the journeying of a vertex every bit its candy for a 3D frame. We didn't cover everything (that would be an enormous commodity!) and nosotros're sure you lot'll have plenty of questions about vectors, matrices, lights and primitives. Burn down them our way in the comments section and we'll do our all-time to respond them all.
Also Read
- Wi-Fi 6 Explained: The Side by side Generation of Wi-Fi
- How CPUs are Designed and Built
- Display Tech Compared: TN vs. VA vs. IPS
Source: https://www.techspot.com/article/1857-how-to-3d-rendering-vertex-processing/
Posted by: urenogotand.blogspot.com


0 Response to "How 3D Game Rendering Works: Vertex Processing"
Post a Comment